Polynomial-time algorithm for approximating the volume of convex bodies

The paper ^[1] is a joint work by Martin Dyer, Alan M. Frieze and Ravindran Kannan.

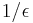The main result of the paper is a randomized algorithm for finding an $\epsilon$ approximation to the volume of a convex body $K$ in $n$ -dimensional Euclidean space by assume the existence of a membership oracle. The algorithm takes time bounded by a polynomial in $n$ , the dimension of $K$ and $1/\epsilon$ .

The algorithm is a sophisticated usage of the so-called Markov chain Monte Carlo (MCMC) method. The basic scheme of the algorithm is a nearly uniform sampling from within $K$ by placing a grid consisting $n$ -dimensional cubes and doing a random walk over these cubes. By using the theory of rapidly mixing Markov chains, they show that it takes a polynomial time for the random walk to settle down to being a nearly uniform distribution.

References

^ M.Dyer, A.Frieze and R.Kannan (1991). "A random polynomial-time algorithm for approximating the volume of convex bodies". Journal of the ACM 38 (1): 1–17. doi:10.1145/102782.102783. http://portal.acm.org/citation.cfm?id=102783.